Diagram 12: Cobweb plot / logistic map

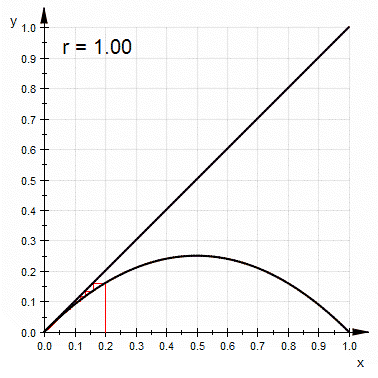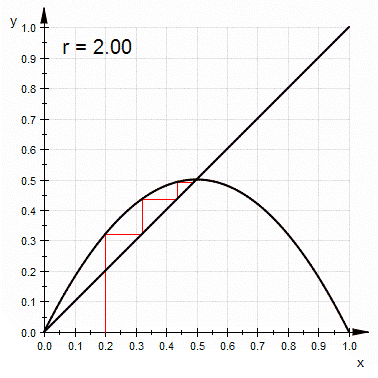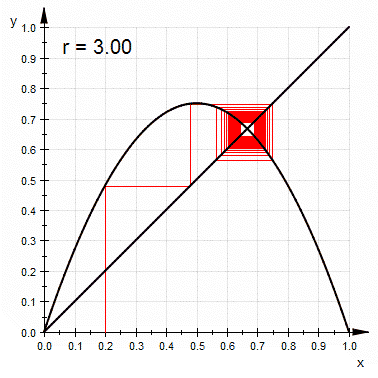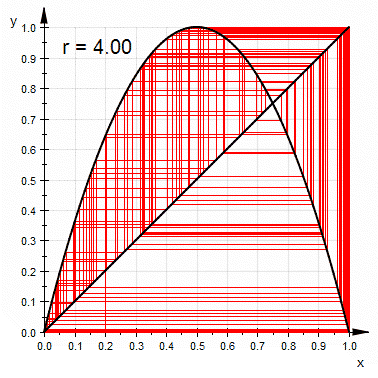
It's a way to graphically calculate iterations of a function. You start with a graph of some function f(x). Then add the diagonal d(x)=x. Given a starting value x, you can find f(x) by going vertically up until you hit the curve of the function.

Before we can start over (that's what iteration is about), we need to convert our y coordinate on the curve to a point on the x axis. To get there, go horizontally to the diagonal. On it, y = x so the new x position is right below on the x axis. The animation below shows lots of paths obtained like that for a famous family of functions i'll talk about in a minute.

This technique can also be found under graphical iteration or Verhulst diagram . That name is in honor of Pierre François Verhulst, who was inspired by Thomas Malthus 'An Essay on the Principle of Population', before he came up with a differential equation to model growth behaviour in 1845. Much later, in 1976, the biologist Robert McCredie May applied the concept to model a time series instead and obtained the much simpler, discrete iteration formula :

f(x) = a * x * (1-x)

http://en.wikipedia.org/wiki/Logistic_map

It's a restricted population growth model where the population x can range from 0 (none) to 1 (every inch inhabited). In plain english it says: The next year's population is a reproduction rate a multiplied by the current years' population x, multiplied by the space currently unused in the environment (1-x).

If you plot this, you'll get a parabola going through x=0 and x=1. It opens downwards and the maximum depends on a. With a little differential calculus (or experimenting) we can see that when a exceeds 4, part of the parabola is above y=1, and that could result in a population greater than one in the next year.

After that 1976 paper the logistic map became very popular as a simple example for chaos . No wonder, it shows most of what can happen in a simple 1 dimensional dynamical system (a lot). It's simplicity makes it an excellent first programming project and graphing a time series can be done in a handful of lines. If you do, i'd like to suggest to try these values for a and stare at the results:

• a = 1.5 approaches a limit from one side
• a = 2.5 approaches a limit from both sides
• a = 3.2 the limit bifurcated, we now have period two
• a = 3.56995 period doubling concludes to practically period infinity, yielding a Cantor set
• a = 3.828 intermittency happens just before...
• a = 3.82843 ...a stable period three appears!

The image is from wikipedia's page on the cobweb plot , you can find a still snapshot there:

http://en.wikipedia.org/wiki/Verhulst_diagram

If you want to know how Robert May got his title as Baron May of Oxford, try this:

http://en.wikipedia.org/wiki/Robert_May,_Baron_May_of_Oxford

More about Verhulst's differential equation can be found here:

http://en.wikipedia.org/wiki/Logistic_function

Characterizing and computing bifurcation and fixed points

We can characterize the behaviour near bifurcation points and from that compute where they are and their values.

a < 3 - converges to (a-1)/a which the solution of f(x)=x a < 1+sqrt(6) - fixed point is unstable since |f'(x)| > 1, instead we get a 2-periodic orbit

These ideas can be extended to higher periods. Instead of looking at the behaviour of f(x) and f'(x) we can study f(f(x)) and its derivative. That way we should be able to find out the values and the exact range of the n-periodic orbits. This works for any iteration depth n, not just for powers of two!

The proportion of the width of two successive bifurcation intervals approaches a numerical value called the Feigenbaum constant.

At the end of

Intermittency

It is suggestive to look at the graphs of f(f(f(x))) near critical values of a to see it break through the diagonal. This illustrates the previous points, but for period 3 it shows a new behaviour:

For example, just before period-3 behaviour appears we get intermittent behaviour. The orbit can be seen to approach period-3 but then breaking out into chaos again, just to begin approaching periodical behaviour again.

a=4: repelling orbits for every order n

For a=4 there are no attracting orbits.

f(x) has two, f^2(x) has four, f^3(x) has eight fixed points, ...

There is a bijection of orbits from the sawtooth map to the tent map, and, by topological conjugacy, from the tent map to the logistic map. Since the sawtooth function is simply a binary shift operator, we can trivially construct orbits of order n. Since some of the bitstrings of length 2^n are cyclically equivalent, i.e. give the same necklace, we get http://oeis.org/A003239 orbits of period n. If we discount repetitions of smaller orbits, we get xxx